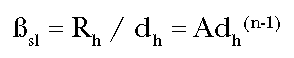BELLE Newsletter Vol 6, No. 1, March 1997
LOW DOSE LINEARITY:THE RULE OR THE
EXCEPTION
Introduction
A recently published paper
by Martha Crawford and Richard Wilson entitled "Low-Dose Linearity: The Rule or
the Exception? " in the journal Human and Ecological Risk Assessment,
Vol. 2, No. 2, 1996 argued that low dose linearity of the dose response curve
might be the rule rather than the exception. While the assumption of low dose
linearity has been widely accepted in concept and implemented in U.S. federal
risk assessment practices for radiation and chemical carcinogens, it has not
been believed to apply to non-carcinogens that have been accepted without
controversy as having thresholds below which no adverse effects would be
expected. However, Crawford and Wilson contend that the concept of low dose
linearity is broadly generalizable and should apply to non-carcinogens as well.
Their article, which urges a reconsideration of how background response is
considered in risk assessment, challenges not only the vast array of current
assertions that low dose linearity is no longer appropriate for low dose cancer
risk assessment but suggests that non-carcinogen risk assessment practices may
need to be reconsidered as well.
While the BELLE initiative has focused
on an assessment of the wide possible range of dose response relationships in
the low dose zone, the BELLE Newsletter has published a series of papers that
have challenged the notion of low dose linearity based on theoretical
foundation, as well as experimental/epidemiological and mechanistic studies.
Thus, given the potentially controversial, yet substantial, nature of the
Crawford and Wilson paper, it was felt that there should be a broad discussion
of this paper since it is at the heart of critical issues in the risk
assessment process. Consequently, Dr. Richard Wilson was contacted and asked to
prepare a shortened form (e.g., 10 pages down from over 30 pages) of the
original article. He also agreed to consider and respond to the comments of a
number of external experts that would be invited to offer independent
commentary on this paper. The reviewers were sent both the original (longer)
version and the shortened form which is now published in the Newsletter. We
trust that you will find this discussion both challenging and
enlightening.
If you have comments on the issue of the Newsletter
please send them to the BELLE office. A decision
will be made whether to publish selected individual responses in a subsequent
issue of the Newsletter and/or to post them on the BELLE website.
If
you are interested in obtaining a copy of the original publication of the
Crawford and Wilson paper in the journal Human and Ecological Risk
Assessment please contact CRC Press, LLC at 1-800-272-7737. Please use the
prompt for journals customer service and ask to speak with Joyce
Lucas.
LOW-DOSE LINEARITY: THE RULE OR THE
EXCEPTION?
Martha Heitzmann1 and Richard
Wilson2
1 Division of Applied Sciences, Harvard
University, Cambridge, MA
2 Department of Physics, Harvard
University, Cambridge, MA;
Tel. (617) 495-3387; Fax (617) 495-0416; Email
wilson@huhepl.harvard.edu
ABSTRACT
In 1976, Crump, Hoel,
Langley, and Peto described how almost any dose-response relationship for
carcinogens becomes linear at low doses when background cancer are taken into
account. This was used by the U.S. Environmental Protection Agency, USEPA, as
partial justification for a regulatory posture that assumes low-dose linearity,
although detailed calculations were not made. The argument depends critically
on the assumption that the pollutant and the background proceed by the same
biological mechanism. In a recently published paper (Crawford and Wilson,
1996), we illustrate the difference between assuming the same and different
mechanisms by discussing the possible dose response relationship for the
leukemia genic response to benzene exposure.We then showed that the same
argument applies to non-cancer endpoints, as well. We discussed the application
to a number of situations: reduction in lung function and consequent increase
in death rate due to (particulate) air pollution; reduction in IQ and hence (in
extreme cases) mental deficiency due to radiation in utero; reduction of
sperm count and hence increase in male infertility due to DBCP exposure. After
concluding that, although the biological basis for the health effect response
is different, in each case low-dose linearity might arise from the same
mathematical effect discussed by Crump et al. (1976), we then examined
other situations and toxic end points where low-dose linearity might apply by
the same argument. Here we review the mathematical support for the argument of
Crump et al., and discuss the policy implications of the generality of
their argument for environmental exposures. In closing, we urge that biologists
and chemists should concentrate efforts on comparing the biological and
pharmacokinetic processes that apply to the pollutant and the
background.
INTRODUCTION
The idea that cancer incidence
might be a stochastic process with the probability of incidence being
proportional to dose dates back at least to the work of Jeffrey Crowther
(1924), who formulated the theory that radiation -induced cancers occur when an
ionized cell becomes malignant and proceeds to multiply. Even if we assume that
most damaged cells are actually repaired by the body's defenses, linearity can
still be maintained, if the fraction of cells repaired is constant with dose.
Since that time, physicists have tended to accept Crowther's suggestion that
cancer incidence is linear with exposure to radiation, but biologists and
physicians have often continued to believe in thresholds.
Crump et
al. (1976) and Guess, Crump, and Peto (1977) pointed out that if a
pollutant produces cancer via the same mechanism by which background cancers
occur, then there results a linear incremental response to the incremental
dose. Even if the biological dose response mechanism has a threshold, or is non
linear, the existence of the background cancers shows that the threshold is
already exceeded by a background pollutant. Then when a small amount of the
same pollutant, or to another pollutant operating in the same way as the first,
is added, an incremental response linear with the incremental dose of pollutant
can result, almost independently of the particular biological mechanism
relating dose and response. This simple and elegant argument follows
mathematically from the fact that the first derivative of a smooth curve is
always finite. The idea was applied to cancer risks, and was used as a partial
justification for the U.S. Environmental Protection Agency's (USEPA) default
assumption of low-dose linearity for regulating carcinogens. Overall, however,
the seminal paper of Crump et al. (1976) has received remarkably little
attention, and few people (not even the EPA) have discussed how the idea should
be applied in practice. At a minimum, the concept of incremental linearity
should shift the focus of discussion from biological thresholds (which are
almost impossible to verify at the levels of interest) to whether the pollutant
and whatever causes the background cancers operate via the same biological
mechanism.
An examination of the risk assessment literature published
during the past twenty years, however, reveals that discussion has remained
focused on trying to identify biological thresholds, rather than biological
mechanisms, for given effects. At the same time, the EPA has continued to
assume a nonlinear, or "threshold," dose-response relationship for regulating
chemicals that are toxic, but not carcinogenic. In recent years, several
researchers have suggested the inadequacy of this approach, demonstrating that
the arguments made by Crump et al. about carcinogens may also be
extended to non-carcinogenic toxins. For several non-cancer adverse health
effects, a no-threshold dose-response mechanism has been suggested (Evans et
al., 1982, Pease et al., 1992). Crawford and Wilson (1996) have
demonstrated that the mathematical effect formulated by Crump et al.
(1976) applies to an array of situations in which a pollutant causes a
non-cancer, or toxic, adverse effect. The one requirement is that there exists
a reasonably large background of the biological effect under consideration, and
that the pollutant acts in the same way as the background. It is evident that
this might be satisfied by a large number of biological effects and pollutants.
The generality of the argument suggests that a linear dose-response
relationship may be the rule, rather than the exception, at the low doses
typical of environmental exposures, even for ordinary toxic (noncarcinogenic)
effects.
INCREMENTAL POTENCY ARGUMENT
In this section we
apply the argument of Crump et al. to any biological endpoint, using
both an analytical and a graphical approach. For the sake of argument, we
assume that the biological response to a dose of a substance is inherently
non-linear, but monotonically increasing, such as depicted in Figure 1. It
might for example be represented by a power law, R = Adn. ( R is
response, A is a constant, d is dose, n is an integer greater than one.) (If
the dose response is not monotonic, or n < 1, the situation becomes more
complex and needs more careful scientific and public policy discussion. This
has not yet been the focus of regulatory discussion.) Figure 1 presents the
particular case of a cubic (n = 3) power function. If there were no background
incidence of the response in question, the dose-response relationship at low
doses would be clearly non-linear, and an infinitesimal increase of dose would
give a negligible increase in response.
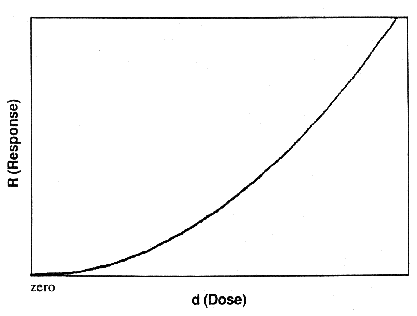
Figure 1. Typical nonlinear,
"threshold", dose-response relationship (R =
Ad3).

Figure 2. Threshold dose-response relationship (R =
Ad3) with axes shifted to R0 and d0. Note that
 R0 is proportional to
R0 is proportional to  d0.
d0.
In
general, if it is assumed that a particular background effect is caused by a
mechanism similar to that caused by the pollutant in question, it follows that
there must exist an "equivalent background dose", d0, to create this
background response, corresponding to R0
=Ad0n, as shown in Figure 2. This "background dose" may
be a background of a different substance so that it would not normally be
considered, but it might be a substance that acts via the same biological
mechanism as the pollutant under discussion. If the dose is increased by an
amount  d due
to anthropogenic (pollutant) activity, the response will increase by an amount
d due
to anthropogenic (pollutant) activity, the response will increase by an amount
 R, so
that:
R, so
that:
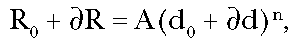 (Eq 1)
(Eq 1)
where A
is a constant greater than zero.
Expanding this for
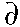 d small (which is
typical of most environmental exposures), we find:
d small (which is
typical of most environmental exposures), we find:
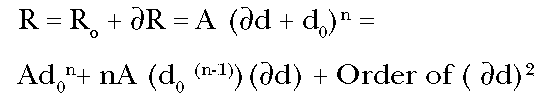 (Eq. 2)
(Eq. 2)
Solving Equation (2) for
dR, we find:
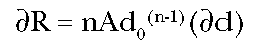 (Eq. 3)
(Eq. 3)
The incremental potency of the toxin,
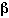 inc, is then equivalent to the slope of the dose-response
curve, or:
inc, is then equivalent to the slope of the dose-response
curve, or:
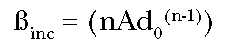 (Eq. 4)
(Eq. 4)
If the dose-response curve is "anchored" by a measured acute response
Rh, corresponding to a high dose dh (including background
dose d0), as is typical of data gathered through laboratory
experimentation, then Rh = Adhn.
The
straight line potency, 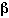 sl, is
derived by drawing a straight line from the response at the high anchoring dose
to the origin:
sl, is
derived by drawing a straight line from the response at the high anchoring dose
to the origin:
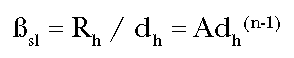
whereas the incremental potency at dose d0 is
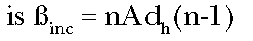 (Eq. 5)
(Eq. 5)
The ratio of the
incremental to straight line potency is then:
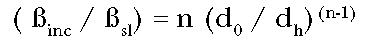 (Eq. 6)
(Eq. 6)
The incremental potency
at the anchoring dose is greater than the straight line potency by the factor
n(d0 / dh)(n-1). In general, if the dose is
close to the background dose (as is typical for environmental exposures) the
incremental potency will be less than the straight line potency (as determined
by data at the higher dose), as seen in Figure 3. It is important to realize
that the coefficient of low dose linearity (the slope of the curve, starting
from R = R0 at d = d0) will not generally be the same as
the coefficient of high dose linearity, as derived from laboratory studies at
acute doses dh. Moreover the low-(incremental) dose slope depends
not only upon the biological dose-response curve but also upon the background
dose level. The value of the ratio is shown as a function of dose in Figure
4.
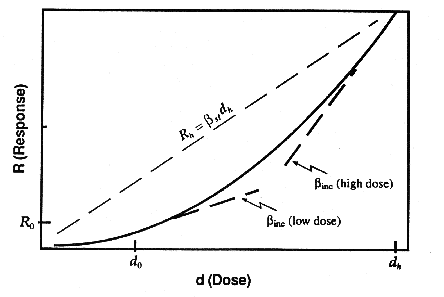
Figure
3. Comparison of slope derived from incremental response model,
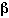 inc,
and that derived by extrapolation from high-dose laboratory data,
inc,
and that derived by extrapolation from high-dose laboratory data,  sl.
Note that often
sl.
Note that often 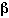 inc <
inc < 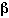 sl.
sl.
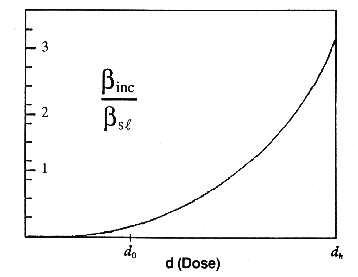
Figure 4. Incremental dose,
di versus Risk Ratio (RR). At low doses, when di =
d0, incremental potency is less than the straight line
potency.
If the response under consideration is the
probability of developing a particular cancer, the above argument is
essentially the argument of Crump et al. But the argument is also
applicable to non-cancer responses, as we recently showed in detail in Crawford
and Wilson (1996). In application to non-carcinogens, the normal curve might
describe the population variability with regard to some biological capacity,
such as fertility or lung function, which is compromised by the effects of a
pollutant (Dockery et al., 1983; Beck, Doyle, and Schachter, 1981;
Links, Kensler, and Groopman, 1995). We argue that, if the resultant deficiency
occurs naturally via the same basic biological mechanism as that through which
the pollutant exerts its effect, then even a small increase in pollutant
increases the number of people with the deficiency. Thus the pollutant elicits
an incremental (and possibly linear) response with even the lowest dose,
irrespective of the biological details of the dose-response relationship,
provided that it monotonically increases. It should be clear, however, that
non-monotonic cases, which might exist if the distribution of the effect in the
population were discrete or bi-modal, would need different treatment.
Often, an epidemiological measurement from an acute exposure, or a laboratory
measurement from a high-dose experiment, fixes a risk ratio (RR), the ratio of
the effect at the dose where it is measured dh, to the background
effect at the assumed background dose d0. Then:
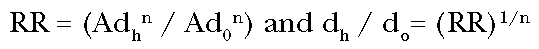 (Eq. 7)
(Eq. 7)
Eliminating the values of
the doses from these equations, the ratio of the incremental potency to the
straight line potency becomes:
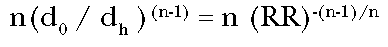 (Eq. 8)
(Eq. 8)
The general requirements for this model are
easily seen: (1) the original, biologically derived, dose-response curve must
be smooth and monotonic; and, (2) the background agent and the pollutant must
act by the same mechanism or receptor in causing the effect. As a restriction
upon the generality of the argument, we note that this argument involves the
dose applied to the organ of concern. Any non-linearity in the pharmacokinetic
relationship between exposure and organ dose remains.
As an example of
the incremental potency argument, consider how the regulation of benzene might
be modified if we assume a non linear biological dose response with two
alternative assumptions about the background. The limited data on leukemia in
humans suggests that benzene carcinogenicity proceeds via a non-linear
dose-response mechanism with toxic effects manifested via metabolites (Lamm
et al., 1989; Thorsland et al., 1988; Paustenbach, Bass, and
Price, 1993). Furthermore, benzene is not a direct mutagen, rendering linearity
even more unlikely. We here assume that the dose-response is a cubic (n = 3)
function, but also make the usual assumption that benzene produces leukemias in
the same way that background leukemias are produced. The risk ratio, at the
dose where the data on benzene are anchored, is given by RR = 12. Then the
incremental potency (near the background dose) is approximately 3/5 of the
straight line potency (as shown in Figure 3). An argument similar to this has
been given for the risk of leukemia from benzene by Thorsland et al.
(1988). To the best of our knowledge this was the first quantitative discussion
using the Crump et al. (1976) idea.
In general, the ratio of
incremental potency to straight line potency is on the order of one, when (3
< RR < 30) and (2 < n < 5), which can justify the present
regulatory approach. However, to the best of our knowledge, this simple
justification has never been given before. Statistical limitations make it
usually impossible to determine directly the dose-response relationship at the
low doses of interest to environmental regulators. However, it may be possible
to determine the linearity (or otherwise) of the intermediate biological
response and this analysis suggests that is a good place for biological
attention.
The usual assumption that background- and pollutant-induced
biological effects proceed by the same biological mechanism may not be correct
in the case of benzene. There is some evidence that benzene-induced leukemias
are always preceded by pancytopenia, which does not occur naturally in the
population to any appreciable extent. If this is the case, background leukemias
must be produced by an entirely different mechanism than benzene-induced
leukemias, and the Crump et al (1976) argument does not apply. Then the ratio
of the incremental potency at a typical environmental dose of 1/50 of where the
straight line potency is anchored becomes 3 X (1/50)2, or about
1/800 (assuming a cubic dose-response). This emphasizes that it is important
not only to measure the magnitude of the biological dose-response relationship,
but also to have some understanding of the underlying biological mechanism(s)
in particular, whether the mechanisms are the same for pollutant- and
background-induced effects. It is also clear that even if the background
and the pollutant effect operate by the same mechanism, the slope of the
dose-response function at low doses can be much lower than the slope at high
doses if the background itself is small.
In Crawford and Wilson
(1996), we further illustrated the incremental potency argument by applying it
to a range of cases: 1) exposure to particulate air pollutants, cigarette
smoke, and coal dust, causing a reduction in lung function which can lead to
premature death; 2) exposure to DBCP, causing a reduction in sperm count which
can increase incidence of male infertility; 3) exposure to radiation
in-utero, causing a reduction in IQ and hence increased incidence of
mental deficiency among children. In each of these cases others have suggested
a linear dose-response relationship, but have not related their suggestion to
the general principle elucidated by Crump et al. In each case it seems
plausible that there is a linear relationship between an environmental
(typically low-dose) exposure and an intermediate biological response which
itself leads to an effect on health. If the biological model is "plausible",
even though possibly not completely understood, we argue that the calculated
risk must be taken seriously (Crawford and Wilson, 1996; Evans, Ozkaynak, and
Wilson, 1992; Hill, 1965). Indeed, if plausibility is taken to require that
every step in the mechanism leading to the toxic effect be clearly understood,
we will fail to describe (and hence predict and prevent) many risks to health.
Even so, we must ensure that a hypothesis is rooted in available data and
knowledge, and be willing to modify our statement of plausibility if and when
new data appear, or we might spend time and money in fruitless chases.
Conclusions
The yearning for binary ways of coping with risks (yes
it is safe/no it is dangerous) finds its way into scientific discourse. Thirty
years ago, although carcinogens were suspected of displaying linear
dose-response relationships, there were few chemicals known to be carcinogens.
In this context, when the EPA was created, the simplest solution seemed to be
to ban those which were known carcinogens (Coulston, 1977), and if one or two
turned out to have net benefits for society, to cope with these exceptions
separately. In recent years, with the availability of more sensitive detection
instruments, it has been shown that about half of all chemicals tested in
animals cause cancer at some dose. Also, some known carcinogens have been shown
to have benefits for society (for example-saccharin or alar). So today the
simple banning solution seems inappropriate. Our extension of this approach to
non-carcinogenic endpoints (Crawford and Wilson, 1996), using the argument of
Guess, Crump and Peto (1976), underscores the inadequacy of this approach to
the regulation of environmental pollutants. In our view, there is no
alternative to openly discussing what level of risk is acceptable and
possible.
Since it is economically and physically infeasible to
identify and avoid exposure to all harmful agents, we must settle for
protecting against the most harmful and the least beneficial. It is
intrinsically distasteful to consider that the health or life of certain
individuals will be sacrificed for economic gain, even though the sacrifice
would be random. It is much more comfortable to espouse the doctrine of zero
risk, and call for biological models. But as has been discussed widely
(Coulston, 1977; Gorman, 1993) the first makes regulations unwieldy and
impractical, and often diverts scarce regulatory funds to protect against
relatively insignificant risks, while the second is ducking the issue, since
"zero risk" is unattainable and a complete biological model for every pollutant
unrealistic. As a society, we must accept and live with the idea that a
necessary part of health risk assessment involves weighing benefits against
costs.
The number of situations where there is a linear dose-response
relationship is likely to be much greater than that given by carcinogens alone,
and suggests a more careful analysis of what risks are acceptable. The EPA, for
example, has set regulations to protect individuals from low levels of
carcinogen, and set an "acceptable" or "de minimis" level of risk of one
in a million per lifetime. If EPA tries to regulate the many non-carcinogenic
end points to the same standard, the system could well be choked. A
re-examination may well be necessary. We have argued that low-dose linearity
may be a common situation for environmental toxins of interest to public
health, rather than the rarity that has historically been assumed. Any
biological endpoint is likely to display this linearity, in proportion to the
extent that this particular endpoint exists in a subsection of society. The
public policy issues that are raised by this argument are inextricably linked
to societal approaches to especially sensitive groups (Devlin 1993).
In
fact, a precedent exists for the application of this type of "acceptable risk"
approach. The Coal Mine Health and Safety Act (U.S. Congress Public Law 91-173,
1969) requires that each miner working at the coal face be tested once every
five years for early signs of CWP. If any sign is detected, the miner is
reassigned to a work site closer to the surface, where exposure to coal dust is
lower. In this way, individuals with greater susceptibility to lung damage are
identified and only allowed to be exposed to a level of acceptable risk.
Clearly, this law recognizes the inter-individual variability which leads to
differences in response. This inter-individual variability is what leads to
there being a response at the population level for any level of
exposure.
Terminology contributes to the traditional bias toward
consideration of individual thresholds rather than of linearity for the
response of a group. When biologists discuss "low doses," they usually mean low
absolute doses, not low incremental doses. Whereas, when we speak of "low
environmental doses," we think of low incremental doses. Since our mission is
to define a dose-response relationship relevant to environmental doses,
attempts to understand the relationship at the origin of the dose-response
curve (as pictured in Figure 1), may be irrelevant from a regulatory point of
view. Instead we should strive to understand the relationship at the
"background dose". In short, any changed paradigm for regulation of
environmental pollutants should not discuss thresholds without discussing
backgrounds at the same time
The arguments in this paper should not be
construed to imply that the authors reject biologically based models. On the
contrary, we welcome biological models, and suggest, by means of the
macroscopic arguments, where a good biological understanding can be most
useful. A biological model is often taken to mean a full understanding of how a
particular "end point," be it lesion or tumor, is produced by the agent
(pollutant) at issue. In situations where we are discussing an "end point" that
occurs naturally with considerable frequency, we suggest that an emphasis on
the more limited questions of whether the pollutant acts in the same way as the
background may be more tractable and therefore more fruitful. Also, the
distinction between the regulatory treatment of carcinogens and non-carcinogens
‹ that only the former has a linear dose-response relationship ‹ is
probably incorrect.
We also reopen the issue of the default assumptions
for regulatory procedure. Although it is usually hard to find a scientific
reason for a particular regulatory assumption, the default assumption that a
carcinogen has a linear dose-response relationship is often considered
plausible. We argue that for many end points it is plausible that a pollutant
acts in the same way as a background, and therefore that low dose linearity
applies for these - although the slope of the dose response at low doses is not
a simple extrapolation from high doses.
Many scientists would consider
it to be plausible (in the absence of contrary evidence) that a pollutant
contributes to many end points. If plausibility is all that is required for
regulation, then including non-cancer end points in the regulatory scheme in
this way could increase the regulatory load many fold, and emphasizes the need
for a logical way of prioritization.
BIBLIOGRAPHY
Beck,
B.J., Doyle, C.A., and E.N. Schachter. 1981. Smoking and lung function. Am.
Rev. Respir. Dis.13:149-155.
Coulston, F. 1977. Tolerance levels can be
set for chemical carcinogens. C&EN, June 27: 34-37.
Crawford, M.
and R. Wilson. 1996. Low dose linearity: The rule or the exception? Human and
Ecological Risk Assessment 2(2): 305-330.
Crowther, J. 1924. Some
considerations relative to the action of x-rays on tissue cells. Proc. Roy.
Soc. Lond.B. Biol. Sci. 96: 207-211.
Crump KS, Hoel DG, Langley CH,
Peto R. 1976. Fundamental carcinogenic processes and their implications for low
dose risk assessment. Cancer Res 36:2973-2979.
Devlin, R. B. 1993.
Identification of subpopulations that are sensitive to ozone exposure: Use of
end points currently available and potential use of laboratory-based end points
under development. Environ. Health Perspec. Suppl. 101(Suppl 4):
225-230.
Dockery, D.W., Berkey, C.S., Ware, J.H., Speizer, F.E., and
B.G. Ferris, Jr. 1983. Distribution of forced vital capacity and forced
expiratory volume in one second in children 6 to 11 years of age. Am. Rev.
Respir. Dis. 128: 405-412.
Evans, J., Ozkaynak, H., and R. Wilson.
1982. The use of models in public health risk analysis. J. Energy and Environ.
1(1): 1-20.
Gorman, C. 1993. Getting practical about pesticides. Time,
February 15.
Guess, H., Crump, K., and R. Peto. 1977. Uncertainty
estimates for low-dose-rate extrapolation of animal carcinogenicity data.
Cancer Res. 37:3475-3483.
Lamm, S.H., Walters, A.H., Wilson, R., Byrd,
D.M., and H. Grunwald. 1989. Consistencies and inconsistencies underlying the
quantitative assessment of leukemia risk from benzene exposure. Environ. Health
Perspect. 82:289-297.
Links, J. M., Kensler, T. W. , and J.D. Groopman.
1995. Biomarkers and mechanistic approaches in environmental epidemiology.
Annu. Rev. Public Health 16:83-103.
Paustenbach D.J., Bass, R.D., and
P. Price. 1993. Benzene toxicity and risk assessment, 1972-1992: Implications
for future regulation. Environ. Health Perspec. Suppl. 101(Suppl 6):
177-200.
Pease, W., Vandenburg, J., and K. Hooper. Comparing
alternative approaches to establishing regulatory levels for reproductive
toxicants: DBCP as a case study. Environ. Health Perspect. 91:141-155.
Thorsland, T.W., Hegner, R.E., Anver, M.R., and P.R. Voytek. 1988. Quantitative
Re-Evaluation of the Human Leukemia Risk Associated with Inhalation Exposure to
Benzene. Report prepared by Clement Associates, Inc., Farfax, VA, and submitted
to the American Petroleum Institute, Washington, D.C.
INVITED COMMENTARIES TO THE HEITZMANN AND WILSON
ARTICLE
James D. Wilson
Senior Fellow, Resources for the Future, Washington, DC; Tel.(202) 328-5099;
Fax (202) 939-3460
In this paper Prof. Richard Wilson and his
colleague, Martha Crawford Heitzmann, have provided us what the profession
expects from him, a provocative treatise on risk management soundly based on
fundamental physical science. The only hazard posed by articles such as this is
that readers may take as science arguments for a sound policy. This paper
advocates assuming that adverse effects from stressors such as airborne
particulates add to background processes, and are thus justifiably treated for
risk management purposes as being estimated by a linear-through-zero
approximation.
Given valuing protection of people's health, this
policy strikes me as sensible, absent information to the contrary. As science,
however, it does not pass muster.
A philosophical introduction: we
should take as "science" our humble attempts to describe as perfectly as we can
the material world and its manifestations. The English physicist and
philosopher John Ziman argues that society values science because it provides
reliable knowledge about the material world (Ziman, 1978). We value this
reliability because it reduces the uncertainty surrounding decisions we need to
make.
Thus it is important for those of us whose work consists of
interpreting science for policy makers to distinguish our attempts to provide
"best estimates" of reality from policy advice that is conditioned by our
understanding of the relevant values and policy frameworks.
I suggest
that in this paper Drs. Heitzmann and Wilson are proffering policy
advice.
I have several reasons for concluding that this is the role
they have adopted.
First, as a scientific proposition, the hypothesis
described by the title cannot be tested. A scientific proposition would have to
be more complex, in order to contain and explain both the examples of
additivity they cite and the exceptions (of which they cite only one). The very
concept of "the rule" is thoroughly value-laden: In whose eyes might something
be the one or the other? Under what circumstances? The authors allude to the
circumstances in which these questions have answers; these circumstances
concern policy decisions.
Second, their conclusion rests on a
mathematical analysis of a special case and a few examples, one an obvious
‹ and acknowledged ‹ exception. For science, the proof of
their proposition is not persuasive. Third, their extension of Crump's
proposition repeats an important, simplifying initial condition that
effectively turns their argument into a syllogism. They, and Crump and his
co-workers (Crump, et al., 1976; cf. also Krewski, et al.,
1995), begin by postulating that the curve describing the relation between
exposure and effect is continuous and monotonically increasing. A relation that
is discontinuous ‹ a step function, for example ‹ will obviously not
produce a straight line when added to any background process. The result will
still be a step function. Heitzmann and Wilson note that such a case has not
received adequate discussion in the science policy community. I wholeheartedly
agree, and call to the attention of BELLE's readers some relevant papers
by Seiler and Alvarez (1994) and myself (Wilson, 1996). Both Seiler and Alvarez
and I assert that uncertainty ‹ "noise" ‹ in the measurements
frustrate empirical testing of the Crump/Heitzmann and Wilson proposition of
low-dose linearity. Seiler and Alvarez go on to argue that predictions of
"risk" smaller than the measurement-noise limit cannot be reliable guides for
policy ‹ and certainly not useful decision-criteria. I have concluded that
the weight of biological evidence favors the proposition that, for individuals,
the exposure-response for non-mutagenic carcinogens will more closely resemble
a step function than a ramp with its toe at [0,0]. The argument rests on the
observation that for all non-mutagenic carcinogens, the rate-limiting step
consists of inducing proliferation in cells in the target organ, a process that
is very tightly controlled, physiologically. The ability to exert control is
capacity-limited; only when the control capacity is exceed will adverse effects
be possible.
Thinking about discontinuous functions leads us into
thinking about some interesting details of biological plausibility, biological
processes, and what our representations of exposure-response actually mean. We
know, for instance, that actual exposures to any pollutant or stressor vary
with time, yet we represent them as being constant. Even the dirtiest, smokiest
cities of China or Mexico have fine days and nasty ones. We infer that
breathing nasty air causes lung damage by comparing the results of doing so
with the results of living where the air is sweet. By definition, breathing
nice air causes no damage. Does one nasty day in one thousand cause damage? Not
so we can tell. One in one hundred? Ditto. One in ten? Experts think it may.
What is the appropriate way to represent "risk" ‹ likelihood of injury,
given predicted conditions ‹ when the putatively damaging exposures are
occasional but the measure of effect integrates many such exposures? Do the
effects really simply add, or is the true representation some complex function
of stress and repair? Biology suggests the latter.
And how nasty, how
dirty must air be to do damage? Will the smoke from one cigarette in the middle
of the South Atlantic harm us? Evidence exists that agriculturists in dry and
sandy areas suffer some lung damage from the dust they breathe over a lifetime;
clearly our species is not perfectly adapted to living in such conditions. But
how far should we go, how stress-free should we strive to become?
I
have gone beyond science. As they did, I have strolled into that domain in
which the dispute over values can no longer be much informed by science,
because here science has past its limits. As science, the proposition they
describe can be given no better than "not proved." As a policy tool, it has
valuable utility in certain contexts.
So, in closing, a comment on that
context.
It is possible crudely to divide chemical/ environmental
decisions into two kinds. One kind of decision can be made on the basis of a
"screening" or "safety" analysis. The other requires a complex analysis
including evaluation of competing benefits, risks, and interests. In the first
kind, the "safety" decision, we as a society have reached general agreement on
how to balance risks and benefits. In the second, in what might conveniently be
called, "value-balancing" decisions, we have not reached such
agreement.
"Safety" decisions include approval of food additives (FDA)
and "Pre-manufacturing Notices" (EPA / TSCA), establishing standards for
drinking-water contaminants and tolerances for pesticide residues in food, and
screening decisions such as the "no action" decision option in Superfund remedy
selection. The analyses done for these decisions rely very heavily on "default"
assumptions and positions. Heitzmann and Wilson's proposal fits very nicely
among these assumptions and positions. For such purposes it is quite
appropriate to adopt a risk-averse and uncertainty-averse position such as they
advocate. We are, after all, very leery of accepting a median position when
uncertainty is high (absent compensations of some kind); our usual practice is
to "be safe rather than sorry."
The "value-balancing" decision class
includes all the high-stakes environmental decisions, such as ambient air
quality standards (for particulates, ozone, etc.), "major" rules such as
regulating categories of emission sources under either Clean Air or RCRA,
Superfund site remedy selections, revoking pesticide licenses, and so on. These
decisions require tough tradeoffs among costs and benefits, to both the public
and various parts of the private sector. People who live in Los Angeles do want
cleaner air, which a lower ozone standard would force, but they also want to
continue to drive their cars. People who live near Superfund sites want them
cleaned up, but also, often, don't want thousands of loads of dirt trucked past
their houses. Those who are affected by these high-stakes decisions deserve and
need to know, as best as science can tell them, what the risk management
tradeoffs represent. Just because we in the risk analysis profession have been
very tardy in providing this information, in most cases, doesn't obliterate our
obligation to do so.
For these conflicted-value decisions, the kind of
"reasonable worst case" default proposed by Heitzmann and Wilson is useful only
as part of a first-iteration screen. Yet for that kind of purpose, it's useful;
we should adopt it.
References
Crump, K. S., D. G. Hoel, C.
H. Langley, and R. Peto, 1976. "Fundamental carcinogenic processes and their
implications for low dose risk assessment." Cancer Research 36:
2973-2979.
Krewski, D., D. W. Gaylor, and W. K. Lutz, 1995. "Additivity
to background and linear extrapolation." In S. Olin, W. Farland, C. Park, L.
Rhomberg, R. Scheuplein, T. Starr, and J. Wilson, eds., Low-dose
Extrapolation of Cancer Risks: Issues and Perspectives. ILSI Press,
Washington, D.C.
Seiler, F. A., and J. L. Alvarez, 1994. "Definition
of a minimum significant risk." Technology: Journal of the Franklin
Institute 331A: 83-95.
Wilson, J. D., 1996. "Thresholds for
carcinogens: a review of the relevant science and its implications for
regulatory policy." Resources for the Future Discussion Paper 96-21. Resources
for the Future, Washington, D.C.
Ziman, J., 1978. Reliable
Knowledge. Cambridge University Press
Robert L. Sielken Jr.
Sielken, Inc., Bryan, TX; Tel.
(409) 846-5175;Fax (409)846-2671
Heitzmann and Wilson correctly
emphasize the importance of considering background phenomena and their
relationship to the assessment of human health risks. There are four
fundamental points that I wish to make; namely, (1) the authors are making two
critical assumptions, (2) numerous (if not most) biological situations fail to
satisfy these assumptions, (3) even if the assumptions were satisfied, they do
not justify the current practice of using high-dose slope values as low-dose
slope values, and (4) interspecies extrapolations should (but currently
frequently do not correctly) incorporate background phenomena.
Assumptions
As the authors themselves note, the relationship between
the shape of the dose-response relationship at high doses and at low doses is
highly dependent upon the two "critical" assumptions being made by the authors.
First, the background dose and the "pollutant" are assumed to have exactly the
same mechanism of action (that is, that the background dose and the pollutant
dose are additive in the dose-response relationship). For example, this means
not just that the background dose and pollutant both cause liver tumors, but
also that they both affect the same cell types, affect the same stage in a
multistage process, and cause the same type of cellular activity (e.g., both
cause the same adducts, both inhibit the same repair processes, or both impact
cell proliferation or apoptosis in the same way).
Second, the authors
assume that the dose-response relationship is monotonic (strictly increasing in
dose).
Biological Reality
There are numerous biological
situations in which the two critical assumptions made by the authors are not
satisfied, and their argument in favor of low-dose linearity is not applicable.
Because cancer and noncancer health effects are often complex biological
processes involving multiple components and multiple stages, the likelihood
that the first assumption of a common mechanism is satisfied is small. Even if
the first assumption is satisfied, the second assumption of monotonicity may
not be satisfied. In an earlier Belle Newsletter (Stevenson et al.
(1994)) and several follow-up papers (Sielken et al. (1995) and Sielken
and Stevenson (1997 a,b)) examples of several mechanisms are given which do not
have monotonic dose-response relationships. In some cases, the non-monotonicity
is due to the interaction between multiple dose-dependent components, such as
cell birth and death rates. In cases in which health is a dynamic balance
between "invaders" and "defenders", there is a large range of dose-response
shapes that are possible, including non-monotonic ones like "hormesis" (the
potential for beneficial effects over certain dose regions). For example, if
small increases in dose above the background dose stimulate (either directly or
through feedback) the defense mechanisms sufficiently, a hormetic non-monotonic
dose-response relationship can easily occur. The recent Third Belle Conference
was wholly devoted to toxicological defense mechanisms and their impact on the
shape of the dose-response relationships.
Practice
Even if
the authors' two critical assumptions are met, the slope of the straight line
from the risk at the background dose to the risk at a high dose may be much
different (usually much greater ) than the slope of the straight line from the
risk at the background dose to the risk at a small incremental dose above
background. This can be easily illustrated using the authors' own example in
which the probability of a slope of the response follows a power law,
R=Adm. In this case, the straight line from the zero risk at dose
zero to the risk at a high dose dh is Adhn-1;
the slope of the incremental risk at a background dose d0 is
nAd0n-1, and their ratio is
(Adhm-1) / (nAd0m-1) =
(dh/d0)m-1/n.
This
ratio can be easily quite large. For example, if the high dose
dh=10d0 and n=3, then the slope of the straight line from
the zero risk at dose zero to the risk at the high dose dh is more
than 33 times greater than the slope of the incremental risk at the background
dose d0. Similarly, if the high dose dh=100d0
instead of dh=10d0, then the high-dose slope would exceed
the low-dose slope by more than 3000 fold.
Thus, even when the critical
assumptions are met, there is no scientific justification for the common policy
(default) of assuming that the slope of the straight line from the risk at the
background dose to the risk at a high dose is a good estimate or surrogate for
the low-dose slope. It is bad enough that the assumptions used to justify the
theoretical possibility of low-dose linearity are often not carefully
considered or critically evaluated in practice. What may be even worse is the
common practice of using the value of a high-dose slope as the value for
low-dose slopes.
Interspecies Extrapolations
There are at
least two current practices related to interspecies extrapolation that are not
discussed by Heitzmann and Wilson but which fail to properly incorporate
background phenomena. Interspecies extrapolations of cancer potencies (or
dose-response relationships in general) should incorporate interspecies
differences in background doses and especially interspecies differences in
background transition rates from stage to stage in multistage
processes.
The current method of calculating the upper bound on the
cancer potency (q1*) from the linearized multistage model assumes
that the background transition rates from stage to stage in a multistage
carcinogenic process in humans are exactly the same as they are in the bioassay
animals. Because several tumorigenic responses in mice and rats occur in organs
with a much higher background rate than in humans and, hence, higher background
transition rates, the failure to incorporate the interspecies differences in
these transition rates often leads to a significant overstatement of human
risk. Sielken and Stevenson (1994) discuss this flaw and its
mitigation.
A second common malpractice occurs when the dose-response
relationship is not strictly linear and there are interspecies differences in
the background doses. Agencies usually convert the animal bioassay dose levels
to so-called "human equivalent doses" (HEDs) by dividing the animal dose levels
by an interspecies conversion factor (e.g., based on body weights to the 3/4
power). After dividing the animal doses by this conversion factor, the human
dose-response model is supposedly obtained by fitting the animal response
frequencies against these HEDs. Unfortunately, because the animal dose assigned
to the controls is zero and not the actual background dose and the zero HED
assigned to the controls during the dose-response model fitting fails to
reflect any interspecies differences in the background doses, the supposed
human dose-response relationship fails to reflect any interspecies differences
in the background doses. This problem can be overcome by fitting the animal
response frequencies to the animal doses and then extrapolating the fitted
dose-response relationship to humans and incorporating the differences between
human and animal background doses in that extrapolation (Sielken,
1989).
Discussion
While the explicit quantification of
low-dose risks would facilitate cost/benefit analyses and regulatory
prioritizations, the frequent misuse of theoretical arguments supporting
low-dose linearity in special situations as a general license to practice
low-dose risk assessment by using high-dose slopes to characterize low-dose
risks results in frequently biased characterizations of those risks.
Furthermore, because the magnitude of the bias can vary by several orders of
magnitude from one chemical to another or from one situation to another, the
bias makes it virtually impossible to even reliably rank the relative risks or
differentiate significant risks from de minimis risks. This leads to exactly
the misallocation of limited health protection resources that the authors wish
to avoid.
The problems associated with past cancer risk
characterizations based on a default assumption of low-dose linearity and the
faulty use of high-dose slope values as low-dose slope values are a good reason
for the public to be concerned about any extension of these flawed quantitative
cancer risk assessment techniques to noncancer health effects.
References
Sielken, R.L. Jr. (1989). GEN.T: A General Tool for
Incorporating Interspecies Extrapolation Information into Quantitative Cancer
Risk Assessment. ACT / SRA Workshop on Inferring Carcinogenic Effects in One
Species from Data on a Different Species. (Copies available from the
author).
Sielken, R.L. Jr. and Stevenson, D.E. (1994). Another Flaw in
the Linearized Multistage Model Upper Bounds on Human Cancer Potency.
Regulatory Toxicology and Pharmacology 21: 270-280.
Sielken, R.L. Jr.,
Bretzlaff, R.S., and Stevenson, D.E. (1995). Challenges to Default Assumptions
Stimulate Comprehensive Realism as a New Tier in Quantitative Cancer Risk
Assessment. Regulatory Toxicology and Pharmacology 21: 270-280.
Sielken, R.L. Jr. and Stevenson, D.E. (1997a). Modeling to Incorporate Defense
Mechanisms into the Estimation of Dose-Responses. Proceedings of the Third
Belle on Toxicological Defense Mechanisms and the Shape of Dose-Response
Relationships. Environmental Health Perspectives Supplement (to
appear).
Sielken, R.L. Jr. and Stevenson, D.E. (1997b). Opportunities
to Improve Quantitative Risk Assessment. Human and Ecological Risk Assessment
(to appear).
Stevenson, D.E., Sielken, R.L. Jr., and Bretzlaff, R.S.
(1994). Challenges to Low-Dose Linearity in Carcinogenesis From Interactions
Among Mechanistic Components As Exemplified by the Concept of "Invaders" and
"Defenders" Belle Newsletter 3 (#2): 1-8.
Myron Pollycove
Usnrc, Washington, DC; Tel. (301)
415-7884;Fax (301) 415-5369
Professor Emeritus, Laboratory Medicine and
Radiology, University of California, San Francisco, CA
Heitzmann
and Wilson use two assumptions to conclude that though biologic dose-response
relationships are probably non-linear, the biological incremental responses of
risk of cancer or other illnesses to low doses of radiation or chemical
pollutants are linear.
The two required assumptions are:
- The biologic response to a dose of substance is
inherently non-linear, but monotonically increasing. Example: R=Adn
- There exists a reasonably large background of a particular biologic effect
(response) that is caused by a mechanism similar to that caused by the
pollutant in question.
The linear adverse biological responses to
low-dose pollutant increments are logically derived by a simple mathematical
analysis of these assumptions.
The authors' emphasize, "...that it
is important not only to measure the magnitude of the biological dose-response
relationship, but also to have some understanding of the underlying biological
mechanism(s) - in particular, whether the mechanisms are the same for
pollutant-and background-induced effects." Their two assumptions
concerning: 1) the biologic dose-response relationship R=Adn, and 2)
the similarity of underlying background and pollutant mechanisms of inducing
negative health effects, need examination to determine whether they are upheld
by significant scientific data.
The first assumption is not supported
by any statistically significant quantitative data. U.S. National Council on
Radiation Protection (NCRP) 121, November 30, l995 states, "...essentially no
human data can be said to prove or even provide direct support for the concept
of collective dose [based on the linear nonthreshold "(LNT) theory] with its
implicit uncertainties of nonthreshold, linearity, and dose-rate independence
with respect to risk."1 Efforts to present low-dose data that
support the LNT theory, i.e. a monotonically increasing risk of cancer, have
led to misrepresentation of their data by the authors of three studies: 1) the
1989 Canadian Fluoroscopy Study,2 2) its 1996 revision in which the
0.10-0.19Sv and 0.20-0.29Sv dose groups are missing,3 and 3) the
IARC Occupational Workers Study.4
Another effort to support
the LNT theory was made in November 1996. The ICRP and the French Society for
Radioprotection under Chairman Roger Clarke, reviewed the 1996 RERF Life Span
Study of Atomic Bomb Survivors Report 12 which includes the 1985-1990 mortality
data.5,6 The ICRP claimed, though the authors of the Life Span Study
did not, that their analysis of this new data showed a statistically
significant increased solid cancer mortality at doses as low as 5 rem.
According to Warren Sinclair, president emeritus of the NCRP and chairman of
the ICRP Committee 1 which analyzes results of health-effects studies, the new
results "vindicate" previous recommendations to lower permissible dose limits
to 2 rem/year for occupational workers and to 0.1 rem/yr for the general
public. "The combination of more data points and a more precise analysis,
Sinclair said, allowed the RERF researchers to state with confidence that
excess cancer risk due to radiation was observed at doses as low as 50
mSv."6
Statistical analysis of the excess solid cancer
deaths following exposures of 5 rem (P=0.11) and 15 rem (P=0.42) demonstrate
that they are not statistically significant; the lowest significant DS86 dose
for increased solid cancer mortality is 35 rem. The correct dose for this
significant increase is considerably greater than 35 rem since the revised DS86
dosimetry used gives estimates for neutron radiation from the Hiroshima atomic
bomb that are lower by an order of magnitude than both the original T65D
dosimetry and the experimental values obtained from neutron activation
measurements at the distances from the hypocenter that correspond to low-dose
exposures.7
While no statistically significant data support
the assumption of monotonic increased risk of cancer with increased low-dose
radiation, in recent decades there has accumulated a considerable body of
contradictory scientific epidemiologic data.
Increased longevity and
decreased cancer death rates have been observed in populations of the U.S.,
China, India, Austria, and the United Kingdom exposed to high natural
background radiation.7 Several recent epidemiologic studies with
high statistical significance have reported that exposure to low or
intermediate levels of radiation are associated with decreased mortality
and/or decreased incidence of cancer:
- Persons
living in the Eastern Urals after radiation exposure from a thermal
explosion.8
- Atomic bomb survivors and residents of an urban area
with radon spas in Japan.7
- U.S. populations exposed to high
residential radon concentrations.9 Figure 5 shows with high
statistical significance, the strong tendency for lung cancer incidence to
decrease with increasing radon exposure in sharp contrast to the incidence
expected from the LNT theory.
- Occupationally exposed U.S. nuclear shipyard
workers.10,11 Table 1 shows a highly statistically significant
decrease in death rates for exposed nuclear workers compared with unexposed
non-nuclear workers (1mSv=0.1r). Nuclear workers also had lower death rates
from leukemia and from lymphatic and hematopoietic cancers but these were not
statistically significant.
- Canadian women who received repeated diagnostic
lung fluoroscopy.2 Figure 6 shows a statistically significant
decrease in breast cancer deaths in women exposed to 15r(0.15Gy) with a typical
U-shaped response to low-dose radiation.
| Table 1.Standardized mortality
ratios for selected causes of death among shipyard workers in the United
States11 |
| Standard mortality ratio (95% CI) |
| Cause of
Death | ³5 mSv | <5 mSv | Non-Nuclear radiation workers |
| All Causes | 0.76 (0.73,0.79) | 0.81 (0.76,0.86) | 1.00 (0.97,1.03) |
| Leukaemia | 0.91 (0.56,1.39) | 0.42 (0.11,1.07) | 0.97 (0.65,1.39) |
| Lymphatic and haemopoietic
cancers | 0.82 (0.61,1.08) | 0.53
(0.28,0.91) | 1.10 (0.88,1.37) |
| Mesothelioma | 5.11 (3.03,8.08) | 5.75 (2.48,11.33) | 2.41 (1.16,4.43) |
| Lung cancer | 1.07 (0.94,1.21) | 1.11 (0.90,1.35) | 1.15 (1.02,1.29) |

Figure 5. Lung cancer mortality rates vs. mean radon
level r0=l pCi/L. in homes for 1601 U.S. counties. Figure b
incorporates the effects of smoking.9
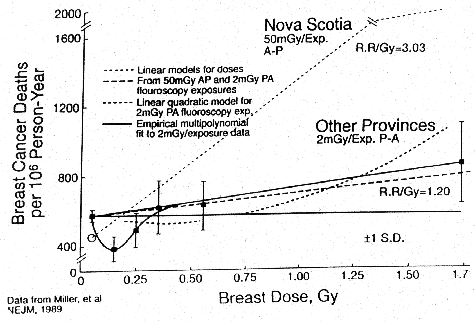
Figure 6. The Canadian
Tuberculosis Fluoroscopy Study of Miller et. al. A graphic plot by E.W. Webster
of the study data showing the authors' "best fit" linear model and
linear-quadratic model relationships. The empirical least-squares best fit is
added and shown.2
Despite almost 40 years of intensive search,
the first assumption of a monotonic biologic dose response (R=Adn)
to radiation is not supported by any statistically significant quantitative
low-dose (e.g. ²20 rem) data. On the other hand, this assumption is
contradicted by the emergence during the past 2 decades of significant data
demonstrating risk decrements in response to low-dose radiation
"pollutant" exposures. Risk increments in response to high doses (e.g.,
³100 rem) are well documented. The authors correctly state, "If the dose
response is not monotonic, or n<1, the situation becomes more complex and
needs more careful scientific and public policy discussion. This has not yet
been the focus of regulatory discussion."
The importance of the second
assumption for the incremental potency argument for low-dose linearity is
stated by the authors. "The one requirement is that there exists a reasonably
large background of the biological effect under consideration, and that the
pollutant acts in the same way as the background." The biological effect of
most concern to radiation protection organizations and the public is cancer
mortality; curiously, not mortality from all causes. Cancer mortality in the
United States is 25% of mortality from all causes, satisfying the requirement
of a large background. But does the "pollutant" radiation act in the same way
to produce cancer as the background?
The complex cell circuitry
signaling for growth, division, and death includes both extracellular factors
and transcription factors. "...the extraordinary detail and duplicate functions
of these circuits are designed so that single disruptions here and there do not
create malignant growth. A cell divides without restraint only when its
circuitry has been disrupted at a number of key points: multiple [persistent]
mutations are required."12 Intrinsic mutations, i.e., mis-unrepaired DNA
alterations occurring in an environment free of mutagens, occur with very high
frequency. "...by fundamental limitations on the accuracy of DNA replication
and repair, ...in a lifetime, every single gene is likely to have undergone
mutation on about 1010 separate occasions in any individual human
being..."13 The additional relentless continual damage of DNA by
reactive oxygen metabolites 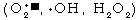 ,
comprising 2-3 percent of all oxygen consumed, and thermal instability,
increases this number to about 1011 mutations per
gene.14,15
,
comprising 2-3 percent of all oxygen consumed, and thermal instability,
increases this number to about 1011 mutations per
gene.14,15
"From this point of view, the problem of cancer
seems to be not why it occurs, but why it occurs so infrequently. Evidently,
the survival of mammals must depend on some form of double-or more than
double-insurance in the mechanisms that protect us from being overrun by mutant
clones of cells that have a selective advantage over our healthy normal cells;
if a single mutation in some particular gene were enough to convert a typical
healthy cell into a cancer cell, we would not be viable
organisms."13
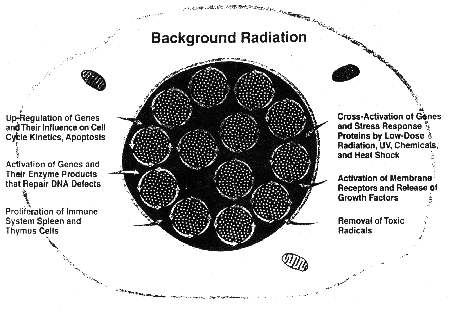
Figure 7. DNA damage control biosystem. Multiple
adaptive responses prevent, repair and remove the 2.4X105 potential
mutations/cell/d produced in humans by reactive oxygen metabolites
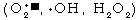 and thermal instability, and each day
remove about 1013 whole body mutations. The length of the arrows
indicate schematically the level of adaptive response activity occurring at
average background level of radiation during youth. The dots inside the nucleus
represent the numerous potential mutations that are successfully prevented,
repaired, and, if still persisting, removed by the adaptive responses
controlling them.
and thermal instability, and each day
remove about 1013 whole body mutations. The length of the arrows
indicate schematically the level of adaptive response activity occurring at
average background level of radiation during youth. The dots inside the nucleus
represent the numerous potential mutations that are successfully prevented,
repaired, and, if still persisting, removed by the adaptive responses
controlling them.
Our survival is dependent upon effective
defense mechanisms that prevent (anti-oxidants, cell cycle control), repair
(DNA repair enzymes) DNA damage, and remove about 1013
mutations daily by cell cycle control, programmed cell death
(apoptosis), necrosis, and the immune system (Figure 7).11,15 The
relatively rare occurrence of cancer under the age of 50 is usually associated
with genetic defects of the biosystem controlling DNA damage. The progressive
age-related decline of biosystem effectiveness is associated with an
exponential increase in the incidence of cancer with the third to the fifth
power of age.13,16-20
A whole body radiation background of
0.1r/year produces about 109 mutations/day.15,21 Exposure to
20r/year would produce about 2x1011 mutations/day. Though this is
insignificant compared to the intrinsic metabolic background of 1013
mutations/day,15 a very small linear incremental risk of cancer
would result theoretically, assuming that the effectiveness of the biosystem
controlling DNA damage remains constant. Heitzmann and Wilson state, "Even
if we assume that most damaged cells are actually repaired by the body's
defenses, linearity can still be maintained, if the fraction of cells repaired
is constant with dose." During the past 15 years studies have shown that the
fraction of cells repaired is not constant, but is increased by low dose
radiation and decreased by high dose radiation. Though the activity of the DNA
damage-control biosystem is decreased by high dose (e.g., ³100r),
high-dose-rate (e.g., ³20r/min) radiation, it adaptively responds with
increased activity to low-dose (e.g., ²20r), low-dose-rate (e.g.,
²1r/min) radiation as well as to low-dose toxic chemical
agents.11,16,22
Low-dose linearity (R=Adn) and
LNT theory (n=1, R=Ad) applied to the risk of cancer are based on two
assumptions: 1) the biological response of cancer to radiation dose is
monotonically increasing, and 2) all mutations, whether induced by ionizing
radiation or other agents, pro
duce a corresponding increase in the
risk of cancer, assuming the fraction of cells repaired is constant with dose.
These assumptions are invalid for they are contradicted, without any support,
by statistically significant low-dose epidemiologic data and they ignore the
operative effect of ionizing radiation on the DNA damage control biosystem.
Emphasis is placed on the relative difficulty of repairing infrequent double
strand breaks (0.4/cell/r low-LET radiation)21 and if unrepaired,
ignoring their daily removal, together with trillions of other
environmental and spontaneous mutations, by the adaptive responses of cell
cycle control, self programmed cell death (apoptosis), necrosis, and the immune
system. Disregarded are the extremely high number of spontaneous mutations and
the adaptive responses to radiation that, until they diminish with age, very
effectively prevent, repair, and remove both the spontaneous and the few
low-dose, low-dose-rate environmental mutations.
Contrary to the
increased risks associated with injury to the DNA damage-control biosystem by
high-dose radiation, this biosystem is stimulated by low-dose radiation to
function even more effectively and decrease the risks of mortality and
cancer. These observations of fundamental biologic cellular functions
contradict the theoretical assumptions based on biophysical concepts
and exclude a LNT dose-response relationship.
Scientific
understanding of the positive health effects produced by adaptive responses to
low-level radiation would result in a realistic assessment of the environmental
risk of radiation. Instead of adhering to non-scientific influences on
radiation protection standards and practice23 that impair health
care and research and waste many billions of dollars annually for protection
against theoretical risks, these resources could be used productively for
effective health measures and other benefits to society.
References
- National Council on Radiation
Protection and Measurements. Principles and Application of Collective Dose
in Radiation Protection. NCRP Report No. 121, NCRP Bethesda, MD;
1995:45.
- Miller AB, Howe GR, Sherman GJ, Lindsay JP, Yaffe MJ,
Dinner PJ, Risch HA, Preston DL. Mortality from breast cancer after irradiation
during fluoroscopic examination in patients being treated for tuberculosis.
N Engl J Med. 1989;321:1285-1289.
- Howe GR, McLaughlin J. Breast
cancer mortality between 1950 and 1987 after exposure to fractionated
moderate-dose-rate ionizing radiation in the Canadian fluoroscopy cohort study
and a comparison with breast cancer mortality in the atomic bomb survivors
study. Radiat. Res. 1996;145:694-707
- Cardis E, Gilbert ES,
Carpenter, L, Howe, G, Kato I, et. al. Effects of low doses and low dose rates
of external ionizing radiation: cancer mortality among nuclear industry workers
in three counties. Radiat. Res. 1995;142:117-132.
- Pierce DA,
Shimizu Y, Preston DL, Vaeth M, Mabuchi K. Studies of mortality of atom bomb
survivors. Report 12, Part I. Cancer:1950-1990. Radiat. Res.
1996;146:1-27.
- Nucleonics Week. Linear nonthreshold model said
vindicated by new data. McGraw-Hill;1996;37(46):1-3.
- Kondo S.
Health Effects of Low-Level Radiation. Osaka, Japan: Kinki University
Press, Madison, WI: Medical Physics Publishing; 1993.
- Jawarowski Z.
Beneficial radiation. Nukleonika. 1995;40:3-12.
- Cohen BL. Test of
the linear no-threshold theory of radiation carcinogenesis in the low dose, low
dose rate region. Health Phys. 1995;68:157-174.
- Matanoski
GM. Health effects of low-level radiation in shipyard workers final
report. Baltimore, MD: DOE DE-AC02-79 EV10095; 1991.
- United
Nations Scientific Committee on the Effects of Atomic Radiation. Sources and
Effects of Ionizing Radiation; UNSCEAR 1994 Report to the General Assembly,
with Scientific Annexes. New York,NY: United Nations;1994; Annex
B:185-272.
- Varmus H, Weinberg RA. Genes and the Biology of
Cancer. New York, NY: Scientific American Library;1993:153.
- Bishop JM, Cairns J, Ellman R, Land H, Ponder B. Cancer, Chapt. 21.
In Alberts B, Bray D, Lewis J, Raff M, Roberts K, Watson JD, eds. Molecular
Biology of the Cell. New York, NY: Garland Publishing;
1989:1187-1218.
- Billen D. Spontaneous DNA damage and its
significance for the "negligible dose" controversy in radiation protection.
Radiat Res. 1990;124:242-245.
- Pollycove M., Feinendegen L.
Quantification of human total and mis/unrepaired DNA alterations: intrinsic and
radiation induced. Unpublished.
- Yamaoka K. Increased SOD activities
and decreased lipid peroxide in rat organs induced by low X-irradiation.
Free Radical Biol Med. 1991;11:3-7.
- Sohal RS, Weindruch R.
Oxidative stress, caloric restriction, and aging. Science.
1996;273:59-63.
- Lithgow GJ, Kirkwood TBL. Mechanisms and evolution
of aging. Science. 1996;273:80.
- Wei Q, Matanoski GM, Farmer
ER, Hedayati MA, Grossman L. DNA repair and aging in basal cell carcinoma: a
molecular epidemiology study. Proc Natl Acad Sci USA.
1993;90:1614-1618.
- Miller RA. The aging immune system: primer and
prospectus. Science. 1996;273:70-74.
- Ward JF. Radiation
chemical methods of cell death. In Fielden EM, Fowler JF, Hendry JH, Scott D,
eds, Proceedings of the 8th International Congress of Radiation
Research, Vol. II. London, England: Taylor & Francis; 1987:162-168.
- Makinodan T, James SJ. T cell potentiation by low dose ionizing
radiation: possible mechanisms. Health Phys. 1990;59(1):29-34.
- Taylor LS. Some non-scientific influences on radiation protection standards
and practice. In Radiation Protection: a systematic approach to safety:
Proc. 5th Congress of the International Radiation Protection Society, Vol.
I. Jerusalem, March l980. Oxford; New York: Pergamon Press; 1980:3-15.
Disclaimer
The views expressed in this paper are those of the
author and do not necessarily reflects the views or policies of the U.S.
Nuclear Regulatory Commission. The U.S. Government has the right to retain a
nonexclusive royalty-free license in and to any copyright covering this
article.
Kenny S. Crump
ICF-Kaiser, Ruston, LA; Tel. (318) 255-4800;Fax (318) 255-4960
The paper by Crawford and Wilson focuses attention on the
"additivity-to-background" argument for low-dose linearity that was first
advanced in Crump et al. (1976). Given that a general belief in
thresholds remains common among scientists, and the enthusiasm that exists
toward the creation of biologically-based dose-response models, it is useful to
reconsider this simple argument for low-dose linearity. Crawford and Wilson are
absolutely right in their basic assertion that it applies equally well to all
heath effects, although Crump et al. originally presented it in the
context of cancer.
Crump et al. argued that if the background
response of a health effect (cancer or otherwise) is caused by a mechanism
similar to that by which a pollutant causes the health effect, then it should
be possible to represent the background response as a response to an equivalent
background "dose", d0, applied to a generalized dose response that
incorporates both the background dose, d0, and the dose, d, of the
pollutant, i.e., the dose response of the pollutant can be expressed as
R(d0 + d), where R is the generalized dose response function for the
health effect produced by the common mechanism, whether due to the pollutant or
to the effective background dose, d0. Although Crawford and Wilson
restricted attention to the case in which R is monotonically increasing, useful
insights can be gained by considering the case in which R is assumed to have a
threshold at some dose, T (Figure 8). If the background health effects are
occurring by the same mechanism as that through which the pollutant acts (i.e.,
if d0 > T), then the response will be approximately linear with
response (i.e., the slope of the dose response curve will be positive) at low
doses. On the other hand, if d0 < T there will be a threshold in
the observed dose-response at the pollutant dose of dT = T -
d0.
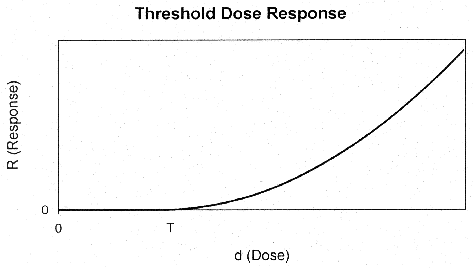
Figure 8. Threshold Dose Response
One important consequence of this argument is that non-linear, non-threshold
responses are effectively ruled out. Note that the only plausible way the low
dose can be non-linear and still non-threshold is for the generalized
dose-response R to be non-linear (e.g., R(d) =Adn, n > 1) and
for d0 = 0. Assuming there is a non-zero effective background dose,
d0, then the low-dose response must be either threshold or linear; a
non-linear non-threshold dose response cannot occur.
All of the above
observations continue to apply if the generalized dose response, R, is U-shaped
(Figure 9), provided the definition of "threshold" is broadly interpreted to
include a beneficial response, and the threshold, T, is associated with the low
point of the generalized dose response. If d0 < T, the response
is beneficial, and if d0 > T, the response is adverse and linear
at low doses. In either case (threshold or u-shaped dose response) the basic
argument for low dose linearity is still valid; if background responses are
occurring through the same mechanism as the dose-related responses (i.e., if
d0 > T), the low-dose response is linear.
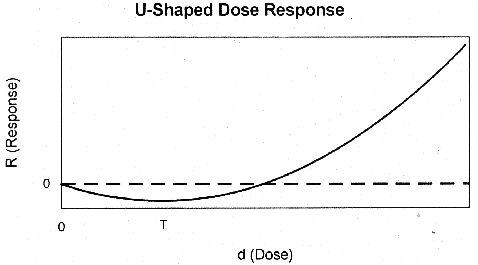
Figure 9. U-Shaped Dose
Response
Crawford and Wilson caution that the argument for
low-dose linearity involves the internal dose, and any "non-linearity in the
pharmacokinetic relationship between exposure and organ dose remains". However,
Richard Peto pointed out a number of years ago in his testimony on the OSHA
cancer policy that the pharmacokinetic relationship between exposure and
internal dose should also be linear at low exposure levels. This observation is
consistent with all pharmacokinetic models (at least all of which I am aware)
that have been developed for specific pollutants. Consequently, the argument
for low-dose linearity applies, not just to the internal dose-response
relationship, but to the exposure-response relationship as well.
The
fact that this simple argument for low dose linearity applies equally to
carcinogenic and non-carcinogenic responses suggests that EPA's former practice
of applying fundamentally different risk assessment approaches to cancer
(assuming a linear dose-response) and non-cancer (assuming a threshold exists)
may not be justified (Crump, et al., 1996). Although EPA's draft cancer
guidelines (EPA, 1996) specify an approach for cancer that is nearer to the
approach generally applied to non-cancer, important differences remain. In a
recent issue of Belle, Crump et al. (1996) proposed that
carcinogens and non-carcinogens be regulated using a common approach that
minimized the use of low dose extrapolation.
Even if low-dose linearity
truly is the rule rather than the exception, as suggested by Crawford and
Wilson, this does not necessarily mean that linear extrapolation from high
doses is always the best approach to risk assessment. Actually, the argument
for low-dose linearity imposes no bounds (other than zero) on the response at
any dose. Estimates of the low-dose slope obtained by linear extrapolation from
high doses could be seriously in error in specific situations.
Based on
the additivity-to-background argument, in order to justify a biologically-based
model of underlying mechanisms that predicts a non-linear low-dose response, it
is necessary to rule out completely the possibility that non-pollutant-related
responses could ever occur via a common mechanism. This would appear to be a
difficult task in many ‹ perhaps most ‹ situations. The argument also
suggests that the shape of the dose
response curve at low doses is
inherently determined by the relationship between background responses and
responses induced by the pollutant. This idea seems to have been largely
ignored by researchers in designing and interpreting experiments with the goal
of understanding low dose risk. Perhaps a fruitful line of research would be to
develop data that could be used to better understand (and perhaps refute) the
additivity-to-background argument for low-dose linearity.
References
Crump K, Hoel D, Langley C, Peto R. 1976. Fundamental
carcinogenic processes and their implications to low dose risk assessment.
Cancer Res 36: 2973-2979.
Crump, KS, Clewell, HJ, Andersen, ME. 1996.
Cancer and non-cancer risk assessment should be harmonized. Belle Newsletter 5,
No. 2/3: 2-4.
Environmental Protection Agency (EPA). 1996. Proposed
the guidelines for cancer risk assessment. EPA/600/BP-92/003.
Dale Hattis
Clark University, CENTED,
Worcester, MA; Tel: (508)751-4603; Fax (508)751-6000
Heitzmann and
Wilson usefully illustrate the critical roles of interactions with background
pathological processes/mechanisms in forming expectations about the likely
effects of incremental exposures to toxicants at relatively low environmental
levels. They also show that one can at least begin the process of estimating
likely low dose effects quantitatively if one has a reasonable amount of
information about the potential for interactions and human interindividual
variability in specific cases.
If I have any complaint about their
summary and their more extensive earlier paper (Crawford and Wilson, 1996), it
is that they have chosen a mathematically tractable power law dose response
formulation for their illustrations, rather than something like a
probit‹which is more directly interpretable in terms of lognormal
variability in susceptibilities to toxic action (and/or) a lognormal
distribution of functional reserve capacities in our diverse human population.
The probit dose response model, long used by toxicologists to analyze acute
animal lethality data, is based on the assumption that there will be a
lognormal distribution of individual thresholds for a specific response. A
lognormal distribution would be expected if there are relatively numerous
sources of individual variability in susceptibility that tend to have
multiplicative interactions. For example, one could well expect individual
differences in the fraction of chemical taken up by a particular medium, rates
of metabolic activation or elimination, and the baseline reserve capacities for
key physiological functions affected by the chemical to all tend to interact
multiplicatively in determining the dose of chemical needed to produce a
specific non-cancer effect in a specific individual. In practice, models
incorporating lognormal susceptibility distributions often describe population
dose response data quite well (Hattis, 1996, 1997) (e.g., see Figures 10 and
11).
Figure 10. Traditional Log Probit Plot of the Excess
% With High  2
Microglobulin Urinary Excretion (Data of Nogawa et al., 1992) Source: Hattis,
1997.
2
Microglobulin Urinary Excretion (Data of Nogawa et al., 1992) Source: Hattis,
1997.

Figure 11. Log Probit Plot of the Percentage of 102
Tested People Who Gave Positive Skin Patch Tests for Chromium (VI) (Data of
Nethercott et al., 1994) Source: Hattis, 1997.
In part because
the field of quantitatively estimating non-cancer effects has been relatively
neglected there is a rich potential for the creative future development of
basic scientific information on individual variability and risk assessment
modeling. In recent work (Hattis, 1997), I have suggested several different
strategies for research and analysis for different responses, depending on
- The distinction between quantal vs continuous
outcome data.
- Whether the causal models appropriate for a specific response
are stochastic vs deterministic on an individual basis.
- The
needs/opportunities to use one-step (simple input-output) models vs multistep
models with intermediate parameters.
Table 2 briefly illustrates these
different strategies.
| Table 2. Strategies for Assessing
Variability in Susceptibility and Predicting Risks |
Outcome
Parameter | One-Step
vs
Multi-Step | Deterministic
vs
Stochastic Process | Example(s) |
| Quantal | One-Step | Deterministic | Traditional
log probit dose response analysis of the percentage of people showing
hypersensitivity responses to dermally applied chromium(VI) solution is
interpreted as a direct measure of the percentage of people who have thresholds
below different doses. |
| Quantal | Multi-Step | Deterministic | Overall
interindividual variability in susceptibility is modeled as a combination of
the variability of component processes-uptake, pharmacokinetic,
pharmacodynamic. E.g. Fish ingestion-methyl mercury uptake-methyl
mercury blood levels-risk of fetal/developmental impairment. |
| Continuous | One-Step | Deterministic | Change in FEV1 from short term
exposures to ozone; Change in measures of kidney function from long term
exposure/uptake/ urinary excretion of cadmium. |
| Continuous | Multi-Step | Deterministic | Lead in house dust-blood lead-impaired
development of IQ in children or elevated blood pressure in adults. |
| Quantal | Multi-Step | Stochastic | 1. Changes in mortality as a function of
cadmium-induced kidney damage; 2. Changes in male fertility as a function of
toxicity-induced changes in sperm count and other sperm quality parameters. 3.
Changes in infant mortality as a function of toxicity-induced changes in birth
weight. |
| Continuous | One-Step | Stochastic | Number and
severity of automobile injuries as a function of blood alcohol
levels. |
| Continuous | Multi-Step | Stochastic | Number and
severity of automobile injuries as a function of defined changes in hazard
recognition and response times induced by alcohol and other neuroactive
substances in experimental subjects. |
| Source:
Modified from Hattis, 1997. |
References
Crawford, M. and Wilson, R. 1996. Low dose linearity: The
rule or the exception? Human and Ecological Risk Assessment 2(2):
305-330.
Hattis, D. 1996. Variability in susceptibility‹how big,
how often, for what responses to what agents? Environmental Toxicology and
Pharmacology, 2: 135-145.
Hattis, D. 1977 in press. Strategies for
assessing human variability in susceptibility, and using variability to infer
human risks. In Characterizing Human Variability in the Risk Assessment
Process, D. Neumann, ed., ILSI Press, Washington, D. C., 1997.
Nethercott, J., Paustenbach, D., Adams, R., Fowler, J., Marks, J., Morton, C.,
Taylor, J., Horowitz, S., and Finley, B. 1994. A study of chromium induced
allergic contact dermatitis with 54 volunteers: Implications for environmental
risk assessment. Occ. Environ. Med. 51: 371-380.
Nogawa, K., Kido, T.,
and Shaikh, Z.A. 1992. Dose-response relationship for renal dysfunction in a
population environmentally exposed to cadmium. In Nordberg, G. F., Herber, R.
FM., and Alessio, L., eds. Cadmium in the Human Environment: Toxicity and
Carcinogenicity International Agency for Research on Cancer, pp.
311-318.
David G. Hoel
Medical University of South Carolina, Charleston, SC;
Tel:
(803)792-2261; Fax (803)792-1123
It is interesting to see both the
continued application of the original Crump et al. (1) paper to cancer
risk and its extension to other biological endpoints. As one of the original
authors of the low-dose linearity paper, I am less enthusiastic than Crawford
and Wilson are over its usefulness. The original paper was written some twenty
years ago without benefit of much of today's biology. What is of concern is
whether or not the original simple idea of background additivity is consistent
with today's biology and whether the concept, if true, has any value for
quantitative risk estimation. Crawford and Wilson appear to answer yes to these
two questions.
The biological complexity is illustrated by the
authors' benzene leukemia example. Pathologists now subdivide leukemias using
the French American British classification. During epidemiological studies, we
are beginning to see differences in the effects of chemicals on these
particular subtypes of leukemia. For example, for acute myelogenous leukemia
Sandler et al. (2) reports a relationship with cigarette smoking and
subtype M2, while Crane et al. (3) reports a high relative risk for
subtype M4 from benzene exposure. Further, in the Taylor et al. (4)
study of acute leukemia, approximately 15% of the human leukemia cases had an
activated ras oncogene. They found that a history of occupational exposures to
solvents increased the risk of ras activated acute leukemias but not for
non-ras acute leukemia.
The example of benzene induced acute leukemia
in man illustrates the existence of multiple pathways and the possibility that
an agent may affect only a particular pathway. The question becomes whether or
not the existence of multiple pathways matters in the linearity argument. If it
does not, then the rarity of an effected pathway should matter.
With
regard to basic cancer dose-response, Ames et al. (5) argues that many
chemicals tested in the NTP animal cancer bioassay induce increased cancer
incidence through cellular proliferation. The idea follows that if this is the
sole biological basis for the cancer increase the carcinogenicity will not
apply at low-dose where the proliferation is not induced by the chemical. Since
cells will die spontaneously the additive background argument would say that
there is low-dose linearity for cellular proliferation. This, I find difficult
to accept.
The next issue at low-doses is the question of hormesis or
adaptive response. Wolff (6,7) has shown with radiation that presumably repair
induction at low-doses will modify the low-dose linearity assumption. This
again illustrates the complexity of the biology and the speculative nature of
the low-dose linearity assumption.
From a quantitative standpoint, I
showed many years ago (8) that very simple pharmacokinetic considerations can
modify risks estimates at low-doses by several orders of magnitude. It seems
then that the additive background argument of Crump et al. (1) 20 years
ago creates a false sense of scientific security in low-dose extrapolation.
What should be said is that low-dose linearity is speculative and it is a
reasonable assumption for public health purposes in those instances where there
is no scientific evidence to the contrary.
References
- Crump, K.S., Hoel, D.G., Langley, C.H., Peto, R.
Fundamental Carcinogensis Processes and Their Implications for Low Dose
Radiation Risk Assessment. Cancer Research 1976;36:2973-2979.
- Sandler, D.P., Shore, D.L., Anderson, J.R., Davey, F.R., Arthur, D., Mayer,
R.J., Silver, R.T., Weiss, R.B., Moore, J.O., Schiffer, C.A., Wurster-Hill,
D.H., McIntryre, O.R. Bloomfield, C.D., Cigarette Smoking and Risk of Acute
Leukemia: Associations with Morphology and Cytogenetic Abnormalities in Bone
Marrow. Journal of the National Cancer Institute 1985;85:1994-2003.
- Crane, M.M., Goodwin, J.E.,Annegers, J.F., Keating, M.J. Is Histology
Subtypea Marker for Environmental Exposures In Acute Leukemia? Cancer
Epidemiology, Biomarkers & Prevention 1992;1:183-188.
- Taylor,
J.A., Sandler, D.P., Bloomfield, C.D., Shore, D.L. Ball, E.D., Neubauer, A.,
McIntyre, O.R., Lui, E. Ras Oncogene activation and Occupational Exposures in
Acute Leukemia. Journal of the National Cancer Institute
1992;84:1626-1632.
- Ames, B.N., Gold, L.S., Shigenaga, M.K., Cancer
Prevention, Rodent High-Dose Cancer Tests, and Risk Assessment. Risk Assessment
1995;16:613-617
- Wolff, S. Aspects of the Adaptive Response to Very
Low Doses of radiation and Other Agents. Mutation Research
1996;358:135-142
- Wolff, S. Faillia Memorial Lecture. Is radiation
all bad? The search for adaption. Radiation Research 1992;131:117-123
- Hoel, D.G., Kaplan, N.L., Anderson, M.W. Implications of Nonlinear Kinetics
on Risk Estimation in Carcinogensis. Science 1983;219:1032-1037
RESPONSE BY:
Martha Heitzmann1 and Richard
Wilson2
1 Division of Applied Sciences,
Harvard University, Cambridge, MA
2 Department of Physics,
Harvard University, Cambridge, MA;
Tel. (617) 495-3387; Fax (617) 495-0416;
Email wilson@huhepl.harvard.edu
We are pleased by the positive note
of the responses to our paper.
Dr James Wilson is right in his
assertion that we "are proffering policy advice". Indeed the whole issue of low
dose linearity is a policy issue, and has been ever since the International
Commission on Radiological Protection suggested it as a Prudent Public Policy
in 1928. But we do not understand his contention that "as science it does not
pass muster". Does he mean this, as we think he should, to apply to all
discussions of possible low dose behavior? If not, we have a serious
disagreement. One of our conclusions is that the underpinning for low dose
linearity for carcinogenesis is not appreciably better than for other medical
end points. A prediction based on indirect data is not as good as a prediction
based on direct data, but it can none the less be a scientific prediction
particularly if a statement of uncertainty is attached. This may just be
semantics; but in the communication of policy recommendations from the
scientist to the managers, the precision in use of words is important.
While we admit that our title was meant to be more provocative than
descriptive, Dr Pollycove has, in our view correctly gone further. He restates
the two assumptions under which low dose linearity can follow: a monotonically
increasing dose response and an understanding of whether the background and the
pollutant act by the same mechanism. He then explains why in his view
radiation, the first agent for which policy makers assumed a linear dose
response does not satisfy these assumptions. It is just this reexamination that
we urge on those responsible for radiation protection. There is still, of
course, another possibility that the basic biological mechanism of radiation
carcinogenesis has a linear dose- response. Pollycove criticizes those who fail
to reexamine radiation carcinogenesis. For example recent (otherwise excellent)
papers by Lubin and Boice (1997) and Riordan (1996) on radon risk assume
(without comment) low dose linearity and in addition many studies assume that
indirect evidence from uranium miners applies to residences. They discount the
direct data at low doses by Cohen (1995) because Cohen made an "ecological"
study. We agree with Pollycove that these assumptions need reexamination. We
urge that the presently sitting BEIR VI committee on radon hazards in
residences at low exposures discuss these assumptions very carefully and also
consider James Wilson's question: are they addressing science or merely policy?
To the extent they are addressing policy, they should note that any errors in
Cohen's arguments can only arise because other causes of lung cancer (such as
smoking) much outweigh the small effect of radon.
We agree with and
welcome the mathematical detail supplied by Crump, Hattis and Seilken. Indeed
we might well have chosen the probit model as a practical example of a
monotonically increasing dose-response relationship. But James Wilson is wrong
when he says that a step function (a threshold) will not produce a straight
line when added to a background process that acts by the same mechanism. It is
not possible to have a finite population background with a step function dose
response unless there is a distribution of sensitivities (perhaps only a narrow
distribution). If that distribution is normal, then the result is the probit
distribution mentioned by Hattis to which the general argument applies.
The most important comment is that of Dr. Hoel who argues that pharmacokinetic
considerations can modify the dose response at low doses. We agree, but note
that this is a discussion of the relation between
organ dose and
applied dose which is another matter entirely. As Crump points out this may
also be linear at low doses. But there can be a change in slope. This can be
crucial if such changes in slope are different between animal (where there are
data) and man where often there are no data. It is also true that the low dose
slope extracted from high dose behavior can be overstated if the background is
small.
We would leave the reader with three important ideas; one is
that low dose behavior of any agent acting on any medical end point can only be
indirectly derived and is to that extent an unproven assumption not a fact.
This is as true for carcinogenesis as for non carcinogens; and another that the
focus of discussion of the mechanisms that provide the indirect data should be
on the relative behavior of pollutant and background. Finally that the
mechanism being discussed only applies when there is a background, and the risk
so derived is a small fraction of background. This is the situation in most
environmental policy issues today.
References
Cohen B.L.
(1995) "Test of the Linear No-Threshold Theory of Radiation Carcinogenesis in
the Low Dose, Low Dose Rate Region" Health physics 68: 157-174
Lubin J.H. and Boice J.D. (1997) "Lung Cancer Risk from Residential Radon: Meta
Analysis of Eight Epidemiological Studies" JNCI 89: 49-57
O'Riordan M. (1996) "Riddle of Radon" J. Radiol. Prot.
16:269-273



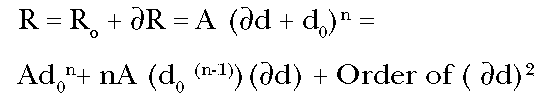 (Eq. 2)
(Eq. 2)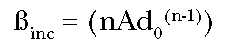 (Eq. 4)
(Eq. 4)